§ 5. Начисление процентов
Если говорить кратко, то начисление процентов — это процесс увеличения задолженности заёмщика перед кредитором с течением времени.
Например, начисление процентов по вкладу выливается в увеличение суммы на счету вкладчика (деньги на счету — это задолженность банка перед вкладчиком). Начисление процентов по кредиту — это увеличение суммы, которую заёмщику нужно будет вернуть в банк.
Процентная ставка
Начисляемые проценты являются платой заёмщика за пользование ссудой — никто просто так не даст пользоваться своими деньгами, точно так же, как никто не даст бесплатно автомобиль на прокат. Размер этой платы определяется с помощью так называемой процентной ставки, которая равна относительному приращению задолженности за единицу времени, то есть за год. Иными словами, если обозначить через S0 первоначальный размер задолженности, а через S(1) — размер задолженности по истечении года, то процентная ставка определяется по формуле
\[ \begin{equation} \tag{5.1} i = \frac{S(1)-S_0}{S_0} \end{equation} \]
Процентная ставка используется для сравнения между собой однотипных ссудных операций: чем выше процентная ставка, тем выгоднее сделка для кредитора. Это становится понятно, если переписать предыдущую формулу следующим образом:
\[\tag{5.2} S(1) = (1+i) S_0 \]
— отсюда видно, что S(1) тем больше, чем больше i.
Пример
Один банк предлагает вклады в рублях под 8% годовых, а другой — под 10%. Если вкладчик имеет на руках 100 тысяч рублей, то, вложив деньги в первый банк, через год он получит сумму
(1 + 0,08) · 100 = 108 тысяч рублей,
а вложив во второй —
(1 + 0,1) · 100 = 110 тысяч рублей.
Разница в 2 тысячи рублей обусловлена разницей в предлагаемых процентных ставках.
Методы начисления процентов
Пытливый читатель должен тут же задаться вопросом: а что будет, если вкладчик заберёт деньги из банка не через год, а через полгода? Какая сумма будет на его счету? Другими словами, по какому принципу происходит начисление процентов? Как, зная только процентную ставку и сумму начального долга, определить размер задолженности в произвольный момент времени?
Как часто бывает в жизни (и как мы уже видели в предыдущем параграфе), в своем желании упростить жизнь человек, напротив, все усложняет до предела. Так люди, далёкие от финансовой математики, придумали два базовых принципа начисления процентов — метод простых процентов и метод сложных процентов.
Миф про метод простых процентов
Метод простых процентов заключается в том, что задолженность заёмщика перед кредитором возрастает с постоянной скоростью. Это значит, что график задолженности является прямой линией, проходящей через точки S0 и S(1) = (1+ i ) S0:
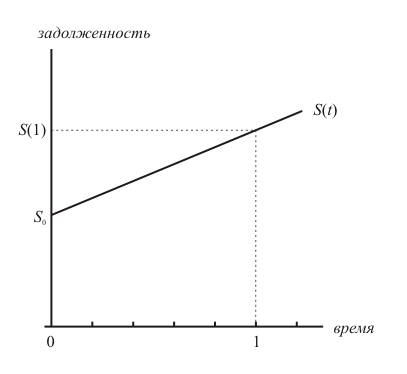
Увеличение задолженности заёмщика по методу простых процентов
Формула, с помощью которой можно найти размер задолженности в произвольный момент времени t, для метода простых процентов имеет следующий вид:
\[ \tag{5.3} S(t) = (1 + it ) S_0\]
(в этом нетрудно убедиться, если подставить в неё значения t = 0 и t = 1).
Пример 1
Допустим, что вкладчик положил сумму 100 тысяч рублей в банк, предлагающий 21% годовых. Если банк использует метод простых процентов для начисления процентов по вкладу, то через полгода на счету вкладчика будет сумма
\(S\left(\tfrac{1}{2}\right) = \left(1 + 0,21 \cdot \tfrac{1}{2} \right) \cdot 100 = 110,5\) тысяч рублей.
Сразу же оговорюсь, пример 2 - незаконный по п.2 ст. 317.1 ГК. Пример приведен с сайта finuch.ru
Пример 2
Для покупки нового телевизора Семен взял кредит в банке в сумме 30000 рублей под ставку 24% годовых сроком на 180 дней. По условиям договора кредит гасится аннуитетными платежами каждые 30 дней. Год для целей расчета процентов будем считать равным 360 дней. Рассчитать график погашения кредита.
| Платеж(денежный поток) | Погашение процентов | Погашение основного долга | Остаток основного долга |
| -30000,00 | 30000,00 | ||
| 5355,77 | 600,00 | 4755,77 | 25244,23 |
| 5355,77 | 504,88 | 4850,89 | 20393,34 |
| 5355,77 | 407,87 | 4947,90 | 15445,44 |
| 5355,77 | 308,91 | 5046,86 | 10398,58 |
| 5355,77 | 207,97 | 5147,80 | 5250,78 |
| 5355,80 | 105,02 | 5250,78 | 0,00 |
Пример 3
Индивидуальный предприниматель Елисей 1 апреля 2022 года взял кредит на сумму 150 000 рублей сроком на 1 год, ставка 25% годовых, проценты выплачиваются ежемесячно без погашения основной суммы долга. Проценты простые. Какую сумму уплатит Елисей за первые 3 месяца?
Решение: в первых 3 месяцах указанного периода 91 день, поэтому Елисей уплатит
\(150 000\cdot \left(\frac{25}{100}\cdot \frac{91}{365}\right)\approx 9 349,32\)
Вот график этого кредита:
| Номер платежа | Дата | Дата в годах | Денежный поток | Погашение процентов | Погашение основного долга | Остаток основного долга |
| 0 | 01.04.2022 | 22 91/365 | -150000 | 150000 | ||
| 1 | 01.05.2022 | 22 121/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 2 | 01.06.2022 | 22 152/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 3 | 01.07.2022 | 22 182/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 4 | 01.08.2022 | 22 213/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 5 | 01.09.2022 | 22 244/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 6 | 01.10.2022 | 22 274/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 7 | 01.11.2022 | 22 61/73 | 3184,93 | 3184,93 | 0 | 150000 |
| 8 | 01.12.2022 | 22 67/73 | 3082,19 | 3082,19 | 0 | 150000 |
| 9 | 01.01.2023 | 23 1/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 10 | 01.02.2023 | 23 32/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 11 | 01.03.2023 | 23 12/73 | 2876,71 | 2876,71 | 0 | 150000 |
| 12 | 01.04.2023 | 23 91/365 | 153184,9 | 3184,93 | 150000 | 0 |
Миф о методе сложных процентов
Смысл метода простых процентов заключается в том, что проценты начисляются всё время на одну и ту же сумму — начальный долг (поэтому скорость начисления процентов постоянна). В отличие от этого, метод сложных процентов характеризуется фразой «начисление процентов на проценты». Это значит, что задолженность заёмщика возрастает в геометической прогрессии: задолженность в предыдущий момент времени служит основой для начисления процентов в следующий момент:
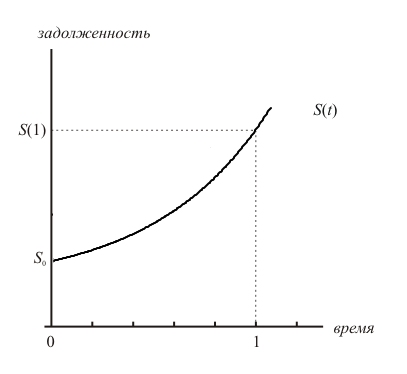
Увеличение задолженности заёмщика по методу сложных процентов
Наглядно представить этот механизм можно следующим образом. Предположим, что вкладчик положил в банк сумму \(S_0\) под процентную ставку i. Тогда через месяц на его счету будет сумма \(S(1) = (1+ i/12 ) S_0\). Если вкладчик решит не снимать деньги со счёта, а снова их вложить с теми же условиями (реинвестировать), то уже через два месяца от даты совершения первого вклада на его счету будет сумма
\[S(2) = (1+ i/12 ) S_1 = (1+ i/12 )^2 S_0\]
Продолжая в том же духе, за n месяцев вкладчик сможет получить сумму
\[S(n) = (1+ i/12 )^n S_0\]
Как видим, сумма вклада возрастает в геометрической прогрессии. Если обобщить этот пример, то можно сказать, что при использовании метода сложных процентов задолженность заёмщика является показательной функцией от времени (показательная функция — это обобщение геометрической прогрессии):
\[\tag{5.4}S(t) = (1+ i /12)^t S_0\]
Пример
Предположим, что вкладчик положил сумму 100 тысяч рублей всё в тот же банк, предлагающий вклады под 21% годовых с ежемесячной капитализацией. Если банк использует метод сложных процентов для начисления процентов по вкладу, то через полгода на счету вкладчика будет сумма
\(S\left(\tfrac{1}{2}\right) = (1 + 0,21/12)^6 \cdot 100\ 000 \approx 110\ 970,24\) руб.
Что такое капитализация процентов? Это процесс увеличения капитала на сумму начисленных процентов. После увеличения капитала проценты начисляются уже на увеличенный капитал.
100 000 + 21%/12 = 101 750
101 750 + 21%/12 ≈ 103 530,63
103 530,63 + 21%/12 ≈ 105 342,42
105 342,42 + 21%/12 ≈ 107 185,91
107 185,91 + 21%/12 ≈ 109 061,66
109 061,66 + 21%/12 ≈ 110 970,24
Обратите внимание: в этом и предыдущем примерах мы неявно полагали, что вклад на полгода имеет продолжительность ½ года. Если бы мы знали точные даты начала и окончания этой финансовой операции, то для получения правильного результата нам бы пришлось вычислять её точную продолжительность в годах по методу «365/365».
Развенчание мифа о методах простых и сложных процентах
Обратите внимание, что смысл метода простых процентов заключается в том, что проценты начисляются всё время на одну и ту же сумму — начальный долг.
Таким образом, если во время вклада происходит любая операция с начальным долгом, считать методом простых процентов нельзя.
Пример. У Вкладчика есть вклад в Банке 100000 руб. на 1 год под 21% годовых с возможностью досрочного снятия и пополнения любой суммы в любое время без изменения процентной ставки. Вкладчик решил закрыть вклад через полгода. Вопрос: какую сумму снимет Вкладчик? Вопрос кажется неоднозначным: мы не знаем по какому методу Банк считает проценты, как выплачиваются начисленные проценты. Очевидно, что при любом действии Заемщика решение данной задачи должно быть справедливым. Предположим, что Банк считает по методу простых процентов, тогда за полгода надо начислить 21%/2=10,5%. Получается 100000+10,5%=110500. Допустим, Заемщик в тот же день передумал и снова открыл такой же вклад с таким же условиями, вложив 110500 руб. Через полгода он закрывает и этот вклад. Получается 110500+10,5%=122102,50 руб. Если бы Заемщик не закрыл первоначальный вклад, то через год он бы получил 100000+21%=121000. Очевидно, что справедливая сумма через полгода первоначального вклада должна быть 10%. Действительно, 100000+10%=110000, 110000+10%=121000 руб. Вспоминаем задачу 5 из первого параграфа.
Предположим теперь, что Банк считает по методу сложных процентов с ежемесячной капитализацией. Без проблем, берем и считаем за месяц
\(\sqrt[12]{1,21}-1\approx 0,016012=1,6012\%\)
100 000+ 1,6012% = 100 000 x 1,016012 ≈ 101 601,19
101 601,19 + 1,6012% = 101 601,19 x 1,016012 ≈ 103 228,01
103 228,01 + 1,6012% = 103 228,01 x 1,016012 ≈ 104 880,88
104 880,88 + 1,6012% = 104 880,88 x 1,016012 ≈ 106 560,22
106 560,22 + 1,6012% = 106 560,22 x 1,016012 ≈ 108 266,45
108 266,45 + 1,6012% = 108 266,45 x 1,016012 ≈ 110 000,00
Итак, мы получили одну и ту же сумму.
Это и есть правильные проценты . Их можно называть, как угодно: правильными простыми и правильными сложными, результат один и тот же. В математике не бывает такого, что одним методом мы получаем одно, а другим методом получаем другое. При любом методе должен получаться один и тот же результат. Например, решение систем линейных алгебраических уравнений может быть получено как методом Крамера, так и методом Гаусса. Результат будет один и тот же, если применимы оба метода.
\[\tag{5.5}S(t) = (1+ i)^t S_0\]
Никаких делений на 12 месяцев или 365 дней, просто показатель степени выражен в годах.
Теперь рассмотрим пример 2 из "простых" процентов.
Для покупки нового телевизора Семен взял кредит в банке в сумме 30000 рублей под ставку 24% годовых сроком на 180 дней. По условиям договора кредит гасится аннуитетными платежами каждые 30 дней. Год для целей расчета процентов будем считать равным 360 дней. Рассчитать график погашения кредита.
| Платеж(денежный поток) | Погашение процентов | Погашение основного долга | Остаток основного долга |
| -30000,00 | 30000,00 | ||
| 5355,77 | 600,00 | 4755,77 | 25244,23 |
| 5355,77 | 504,88 | 4850,89 | 20393,34 |
| 5355,77 | 407,87 | 4947,90 | 15445,44 |
| 5355,77 | 308,91 | 5046,86 | 10398,58 |
| 5355,77 | 207,97 | 5147,80 | 5250,78 |
| 5355,80 | 105,02 | 5250,78 | 0,00 |
Все очень просто: Семен взял и захотел частично досрочно внести платеж, оставив все следующие платежи без изменения, кроме последнего. Если это простые проценты, то последний платеж будет меньше на простые проценты от частично досрочного платежа, если сложные, то последний платеж будет меньше на сложные проценты с ежемесячной капитализацией от частично досрочного платежа.
| Платеж(денежный поток) | Погашение процентов | Погашение основного долга | Остаток основного долга |
| -30000,00 | 30000,00 | ||
| 6355,77 | 600,00 | 5755,77 | 24244,23 |
| 5355,77 | 484,88 | 4870,89 | 19373,34 |
| 5355,77 | 387,47 | 4968,30 | 14405,04 |
| 5355,77 | 288,10 | 5067,67 | 9337,37 |
| 5355,77 | 186,75 | 5169,02 | 4168,35 |
| 4251,72 | 83,37 | 4168,35 | 0,00 |
Итак, Семен взял и заплатил через месяц после получения кредита на 1000 рублей больше. Сэкономил он на последнем платеже 5355,80-4251,72=1104,08
А это как раз сложные проценты:
\(1000\cdot (1+24\%/12)^5 ≈ 1104,08\)
Если бы это были простые проценты, то экономия составила бы:
1000 x (1+24%/12*5) = 1100
Итак, мы видим очень большой обман: предлагают сложные проценты под видом простых, да еще и никаких простых и сложных процентов вообще не существует.
Рассмотрим, насколько же обманули Семена (в случае, если он досрочно не погашал)
| Платеж(денежный поток) | Погашение процентов | Погашение основного долга | Остаток основного долга |
| -30000,00 | 30000,00 | ||
| 5355,77 | 542,63 | 4813,14 | 25186,86 |
| 5355,77 | 455,57 | 4900,20 | 20286,66 |
| 5355,77 | 366,94 | 4988,83 | 15297,83 |
| 5355,77 | 276,70 | 5079,07 | 10218,76 |
| 5355,77 | 184,83 | 5170,94 | 5047,82 |
| 5355,80 | 91,30 | 5264,50 | -216,68 |
На 216,68 руб.
Точно такой же эксперимент вы можете повторить с примером 3 "простых" процентов. Мы еще к нему вернемся. Дело в том, что законодатель привел прекрасную возможность определить, являются это сложными процентами, или не являются.
Это называется ПСК: если убрать все комиссии и прочие платежи и подсчитать ПСК, то при сложных процентах ПСК будет равна (или почти равна) ставке по кредиту. Мы это подробнее будем обсуждать в следующих параграфах, так вот - в примере 3 "простых" процентов ПСК равна 25,007%, то есть почти равна 25%. Почти - это потому что в годах и месяцах разное количество дней, но я уточнил эту функцию.
Итак, самый важный факт: правильные проценты - единственно возможный вариант. Нет никаких ни сложных, ни простых процентов. Есть правильные.
При этом правильные проценты совпадают со сложными при ежегодной капитализации с годовой процентной ставкой.
Правильные проценты имеют не вид прямой пропорциональности, а экспоненциальный.
Поэтому, чем быстрее вы расплатитесь с кредитом, тем больше выиграете с экспоненциальным ростом. Не верьте тому, что кредиты с простыми процентами, их простые проценты являются сложными, а сложные имеют еще более высокую экспоненту, чем правильные.
Правильными процентами аннуитетные платежи, как хочешь, так и считай: хочешь - сначала погашается основной долг, потом проценты, хочешь - сначала проценты, потом основной долг, хочешь - вообще без разделения на проценты и основной долг, хочешь - правилом торговца, хочешь - актуарным способом, хочешь - разбей кредит на части, первая часть погашается одним платежом через месяц, вторая часть одним платежом через два месяца и т.д. - всё равно получится один и тот же результат. При этом как угодно можно досрочно погашать при постоянной ставке, и эффективная процентная ставка не изменится. При правильных процентах, если нет комиссий и прочих платежей, эффективная процентная ставка всегда равна ставке по договору (без учета выходных и праздничных дней и отсрочки платежа (при отсрочке платежа надо считать на дату погашения процентов, а не на дату фактического погашения)).
При правильном расчете "365/365" проценты начисляются по формуле
\(p_i=K_{i-1}((1+r)^{D_i-D_{i-1}}-1)\)
p - сумма начисленных процентов, руб.
Ki-1 - остаток вклада на предыдущем этапе, руб.
r - годовая процентная ставка, доли единицы, например, 10%=0,1
\(D_i=y_i+{d_i+[30,56m_i]-30-[0,1m_i+0,7](367-j_i) \over j_i}\)
yi - год
di - день
mi - месяц
\(j_i = 365+\left(\left[{y_i \over 4}\right]-\left[{y_i-1 \over 4}\right]\right) - \left(\left[{y_i \over 100}\right]-\left[{y_i-1 \over 100}\right]\right) + \left(\left[{y_i \over 400}\right]-\left[{y_i-1 \over 400}\right]\right) \)
[x] - наибольшее целое число, не превышающее x.